Reinforcement Learning Problem Formulation

• Markov Chain (MC)
  • Define (fully observable) states and memoryless (i.e., Markovian) state transitions
• Markov Reward Process (MRP)
  • Indicate preferences through a reward function
• Markov Decision Process (MDP)
  • Include decisions that can be controlled by an agent's policy
• Partial Observable MDP (POMDP)
  • Deal with situations where the true state information isn't available

Markov Chain (MC)

• Markov Property: the current state determines the state transition probability, regardless the history (i.e., memoryless).
• The state transition can be deterministic or stochastic.
• \(\mathrm{MC}=(\gS, P)\)
  • States: \(\vs\in\gS\)
  • State transition function: \(P(\vs'|\vs)\)

Markov Chain, from Wikipedia.

Markov Reward Process (MRP)

• Indicate preferences through reward signals.
• \(\mathrm{MRP}=(\gS, P, R)\)
  • States: \(\vs\in\gS\)
  • State transition function: \(P(\vs'|\vs)\)
  • Reward function: \(R(r|\vs,\vs')\)
    • rewards can be defined for each state transition (i.e., edges)
    • or can be defined for each state (i.e., vertices)

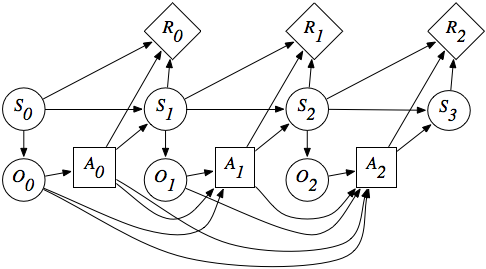
Markov Decision Process (MDP)

• Include decisions that are controlled by an agent's policy.
• Involves an agent with its policy \(\pi(\va|\vs)\).
• The agent's goal is to update its policy so as to maximize the total reward (return).
• \(\mathrm{MDP}=(\gS, \gA, P, R)\)
  • States: \(\vs\in\gS\)
  • Actions: \(\va\in\gA\), where \(\va\sim\pi(\va|\vs)\)
    • Note that \([\text{no action}]\) is also an action.
  • State transition function: \(P(\vs'|\vs,\va)\)
  • Reward function: \(R(r|\vs,\va,\vs')\)
    • rewards can be defined for each state transition (i.e., edges)
    • or can be defined for each state (i.e., vertices)

Markov Decision Process, from Wikipedia.

Partial Observable MDP (POMDP)

• Include an observation function \(O(\vo|\vs)\)
• Agent does not observe the full state features, but can utilize either:
  • the current observation \(\pi(\va|\vo_t)\),
  • the observation history \(\pi(\va|\vo_{0:t})\), or
  • the action-observation history \(\pi(\va|\vh_t)\), where \(\vh_t=[\vo_0,\va_0,\dots,\vo_t,\va_t]\).
• The true state may be approximated by observations based on frame stacking, RNNs, transformers, etc.

SideNote: Markov Chains vs. Markov Decision Processes is analogous to Hidden Markov models (HMM) vs. POMDPs. ¹

POMDP, from Section 9.5.6 of Artificial Intelligence: Foundations of Computational Agents.

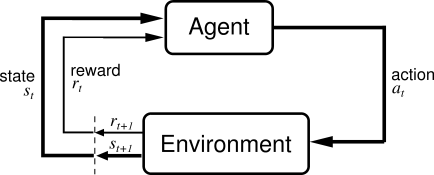
The Agent-Environment Interface

• Training Phase of (Online) RL
  • Agent collects experiences/data \((\vs_t, \va_t, r_{t+1}, \vs_{t+1})\) by exploring the environment, and learn a policy from it.
  • The state transitions & rewards can only be observed through sampling.
• Testing Phase of (Online) RL
  • Agent applies the best learned policy.

The Agent-Environment Interface, from Section 3.1 of Reinforcement Learning: An Introduction.

Examples

Formulating tasks as MDPs for RL. Note that these are just minimal examples, where the actual formulation can be much more complicated.

1. Classification

• Goal: Maximize accuracy.
• State: Input Image \(\vx\).
• Action: Dog or Cat.
• Reward: \(+1\) if correct, \(+0\) otherwise.

2. Shortest Path

• Goal: Minimize total distance.
• State: Current vertex.
• Action: Move along an edge.
• Reward: \((-1)\cdot\text{[edge weight]}\) for each step.

3. Console Game

• Goal: Maximize total score.
• State: Current game screen.
• Action: Game controls (Up, down, left, right, jump, etc.)
• Reward: Immediate score.

4. Robot Control

• Goal: Control robot to perform tasks.
• State: Joint angles, camera images, etc.
• Action: Target joint angles, etc.
• Reward: \(+100\) for each completed task, \(-1\) for each timestep.

---

1. See the topic on Markov Chain on Wikipedia. ↩

Comments