Low-rank adaptation (LoRA)
Goal: Reduce fine-tuning cost by injecting trainable rank decomposition matrices.
Contribution: Reduce the number of trainable parameters by 10,000 times and the GPU memory requirement by 3 times, while introducing no additional inference latency.
Concept
- Hypothesize that the change in weights during model adaptation has a low intrinsic rank.
- For many deep learning tasks with a heavily over-parametrized neural network, the learned neural network will enjoy low-rank properties after training. (Oymak et al., 2019)
- For a pre-trained weight matrix
- This study is limited to only adapting the attention weights (
Architecture of LoRA, from Figure 1 of Hu et al., 2022.
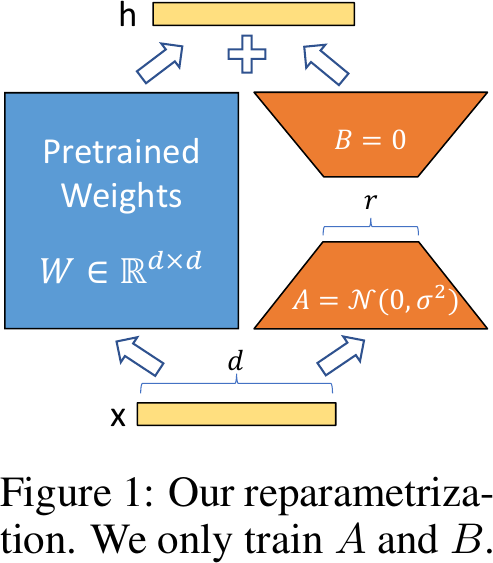
Advantages
- A Generalization of Full Fine-tuning. Recovers the expressiveness of full fine-tuning by setting
- No Additional Inference Latency. Pre-compute
- Lower hardware requirements. Reduce the number of trainable parameters by 10,000 times and the GPU memory requirement by 3 times.
Still have limitations such as difficulties on batching inputs of different downstream tasks.
Related Works
Some drawbacks of other fine-tuning methods:
-
Adapter Layers. Keep the parameters of the pre-trained model frozen. Add two adapter layers per transformer block, and only update these adapter layers during fine-tuning.
- No direct ways to bypass the extra compute in adapter layers.
- The small bottleneck in the adapter layers limits hardware parallelism, increasing latency.
Architecture of the adapter module, from Figure 2 of Houlsby et al., 2019.
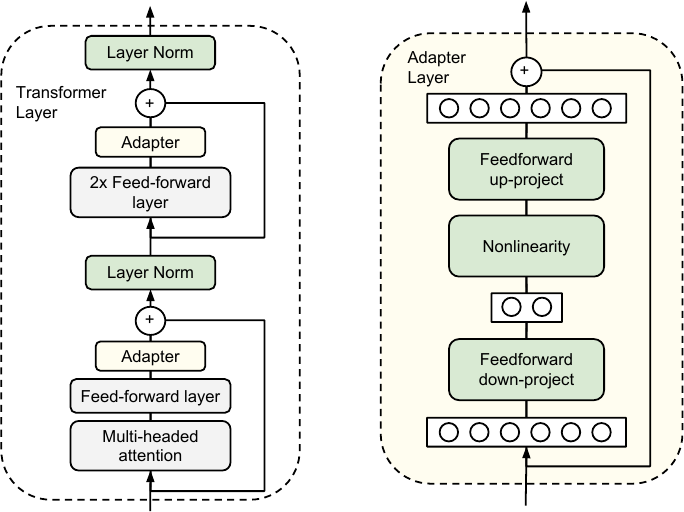

-
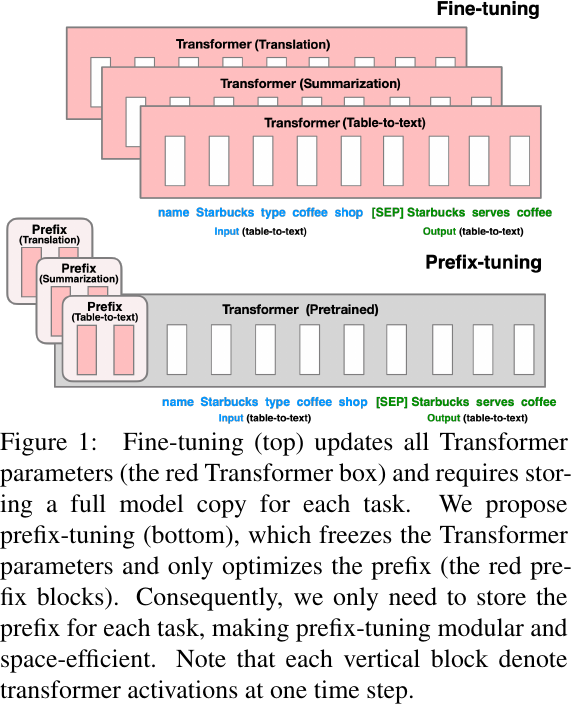
Prefix Tuning. Keep the parameters of the pre-trained model frozen. Prepends a sequence of continuous task-specific vectors (i.e., prefix) to the input sequence, and only update these vectors (i.e., soft prompt) during fine-tuning.
- Difficult to optimize, its performance changes non-monotonically in trainable parameters.
- Reduces the sequence length available for downstream tasks.
Prefix-Tuning, from Figure 1 of Li et al., 2021.
Experiments
Benchmark
Inference Latency, from Table 1 of Hu et al., 2022.

Performance, from Table 4 of Hu et al., 2022.
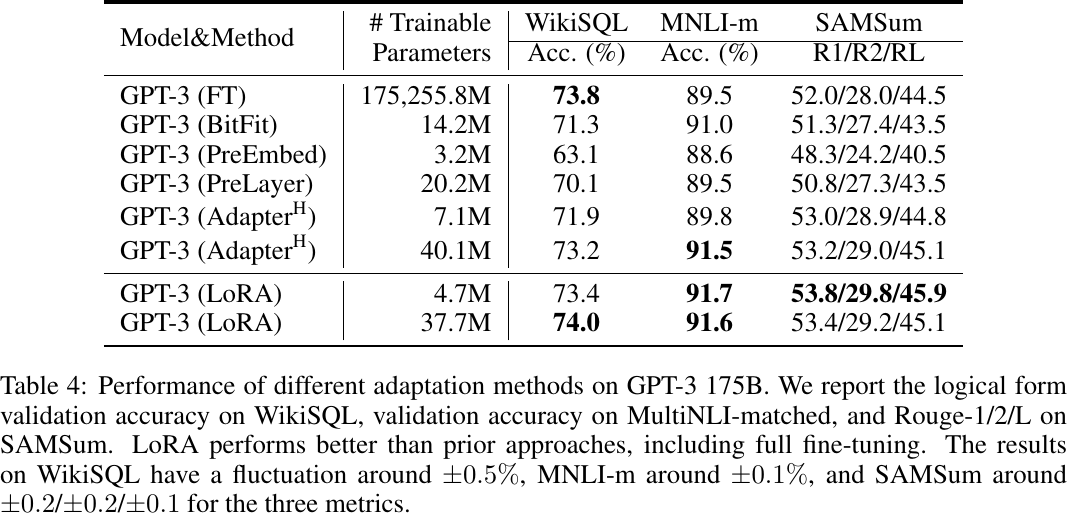
Analysis
-
Which weight matrices in Transformer should we apply LoRA to?
Applying LoRA to different types of attention weights, from Table 5 of Hu et al., 2022.
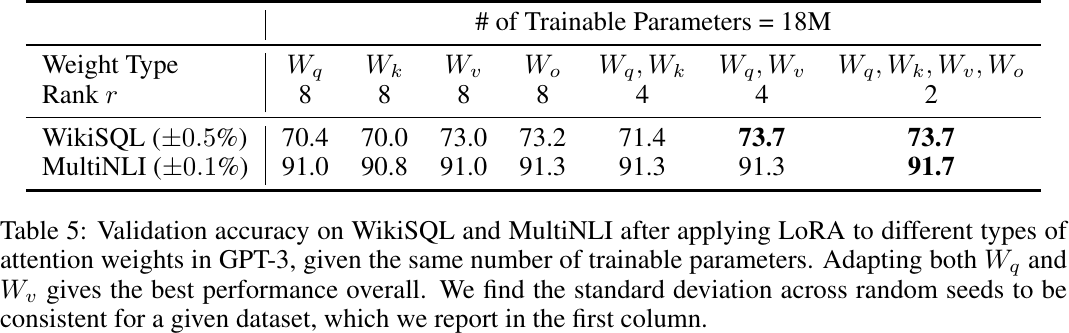
Apply LoRA to
-
Optimal rank
Applying LoRA with different ranks, from Table 6 of Hu et al., 2022.
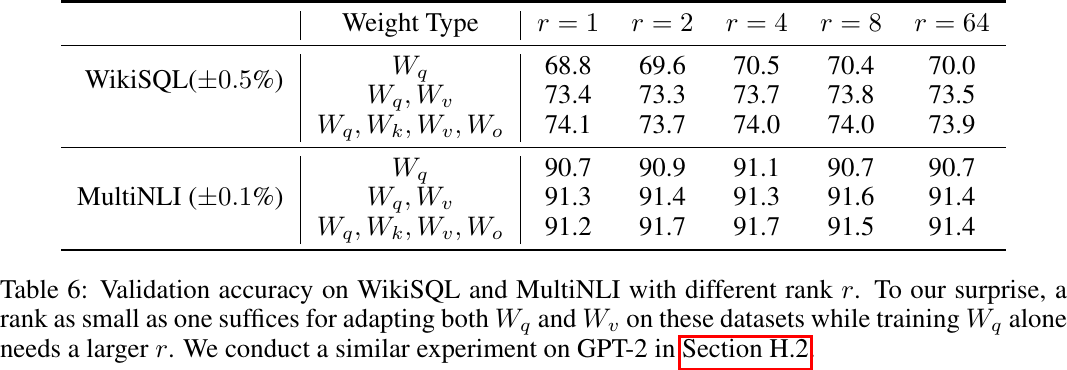
Apply LoRA with
Applying LoRA with different ranks, from Table 18 of Hu et al., 2022.
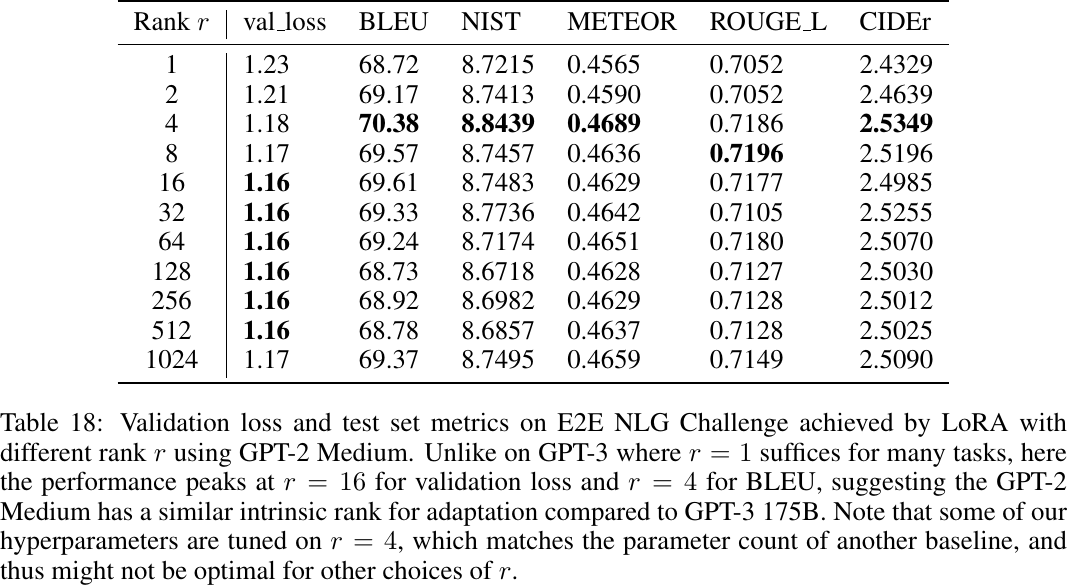
-
Does
Settings:
- Learn adaptation matrices
- Perform singular value decomposition (SVD) and obtain the right-singular unitary matrices
- Use Grassmann distance
Subspace similarity between
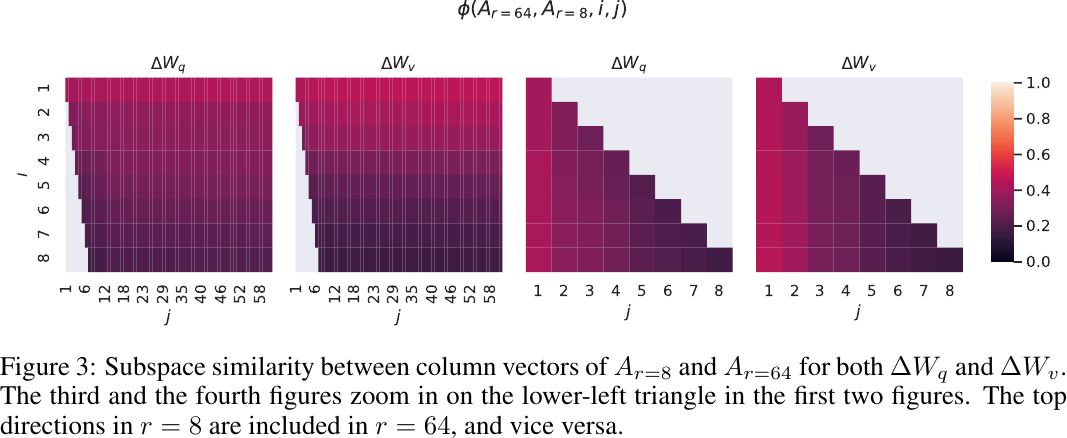
Observations:
- Top singular vector overlap significantly between
- These top singular-vector directions are the most useful, while others contain mostly random noises.
Subspace similarity between two
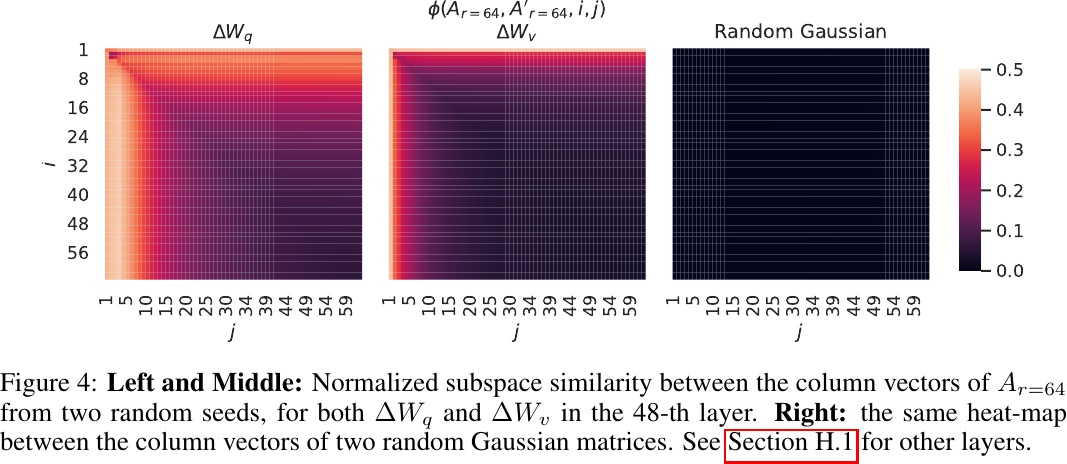
Observations:
- Similarly, the top singular-vector directions are the most useful, while others contain mostly random noises.
Settings:
- Project
Correlation between

Observations:
- Instead of repeating the top singular directions of
- The amplification factor is rather huge:
- Conclusion. The low-rank adaptation matrix potentially amplifies the important features for specific downstream tasks that were learned but not emphasized in the general pre-training model.
Subspace similarity between
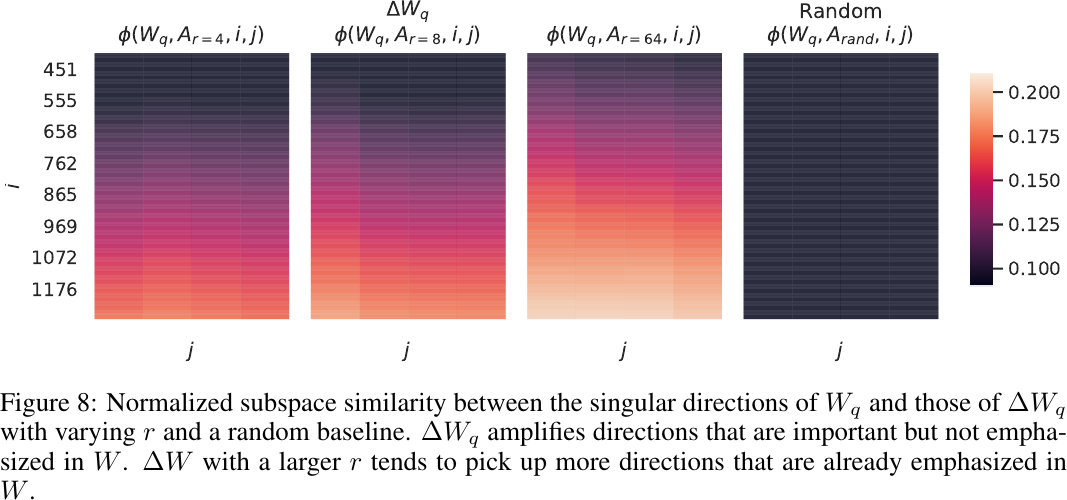
- Learn adaptation matrices
Official Resources
- [ICLR 2022] LoRA: Low-Rank Adaptation of Large Language Models [arxiv][code][paper][video] (citations: 203, 253, as of 2023-03-22)
Community Resources
Low-Rank Adaptation of Large Language Models (LoRA), by HuggingFace