Generative Modeling Overview: a Probabilistic Perspective

$$$$

Goals and Traits of Generative Models

• Density Estimation: pointwise evaluation of $p_{\theta }(\mathit{x})$.
• Data Generation: generating new samples $\mathbf{x}\sim p_{\theta }(\mathit{x})$.
  • Conditional Generation: $\mathbf{x}\sim p_{\theta }(\mathit{x}|\mathit{c})$ for some condition $\mathit{c}$.
  • Imputation: ${\mathbf{x}}_m\sim p_{\theta }({\mathit{x}}_m|{\mathit{x}}_o)$ for some partially observed data ${\mathit{x}}_o$.
• Training Target: the gradient of the loss ${\mathrm{\nabla }}_{\theta }L(\theta )$ should be tractable.
  • Corresponding Metrics: (Forward) KL-divergence $D_{\mathrm{KL}}(p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}||p_{\theta })$, etc.
• Latents: whether latent variables $\mathit{z}$ are introduced, potentially enabling latent interpolation and arithmetics.
• Architecture: whether there are architectural restrictions on the neural network when modeling $p_{\theta }(\mathit{x})$.

Note

• Supporting fast pointwise evaluation of $p_{\theta }(\mathit{x})$ does not necessarily allow fast sampling $\mathbf{x}\sim p_{\theta }(\mathit{x})$, and vice versa.
• Tractable training target $L(\theta )$ does not necessarily allow fast pointwise evaluation of $p_{\theta }(\mathit{x})$ or fast sampling $\mathbf{x}\sim p_{\theta }(\mathit{x})$.
• Likelihood (MLE) is often uncorrelated with the perceptual quality of the samples (images, sound, etc.) ¹

Discussion

How can we parameterize $p_{\theta }(\mathit{x})$ for high-dimensional input, while allowing us to sample from it?

Considerations:

• Can we perform pointwise evaluation of $p_{\theta }(\mathit{x})$?
• (Required) Can we sample from $p_{\theta }(\mathit{x})$?
• (Required) Can we efficiently compute the gradient of the loss?
• Should we introduce a latent variable $\mathit{z}$?
• How can we design the model architecture to satisfy the restrictions?

Taxonomy of Generative Models

Overview of different types of generative models, from Fig.1 of What are Diffusion Models? by Lilian Weng, and from Fig.20.1 of Probabilistic Machine Learning: Advanced Topics.

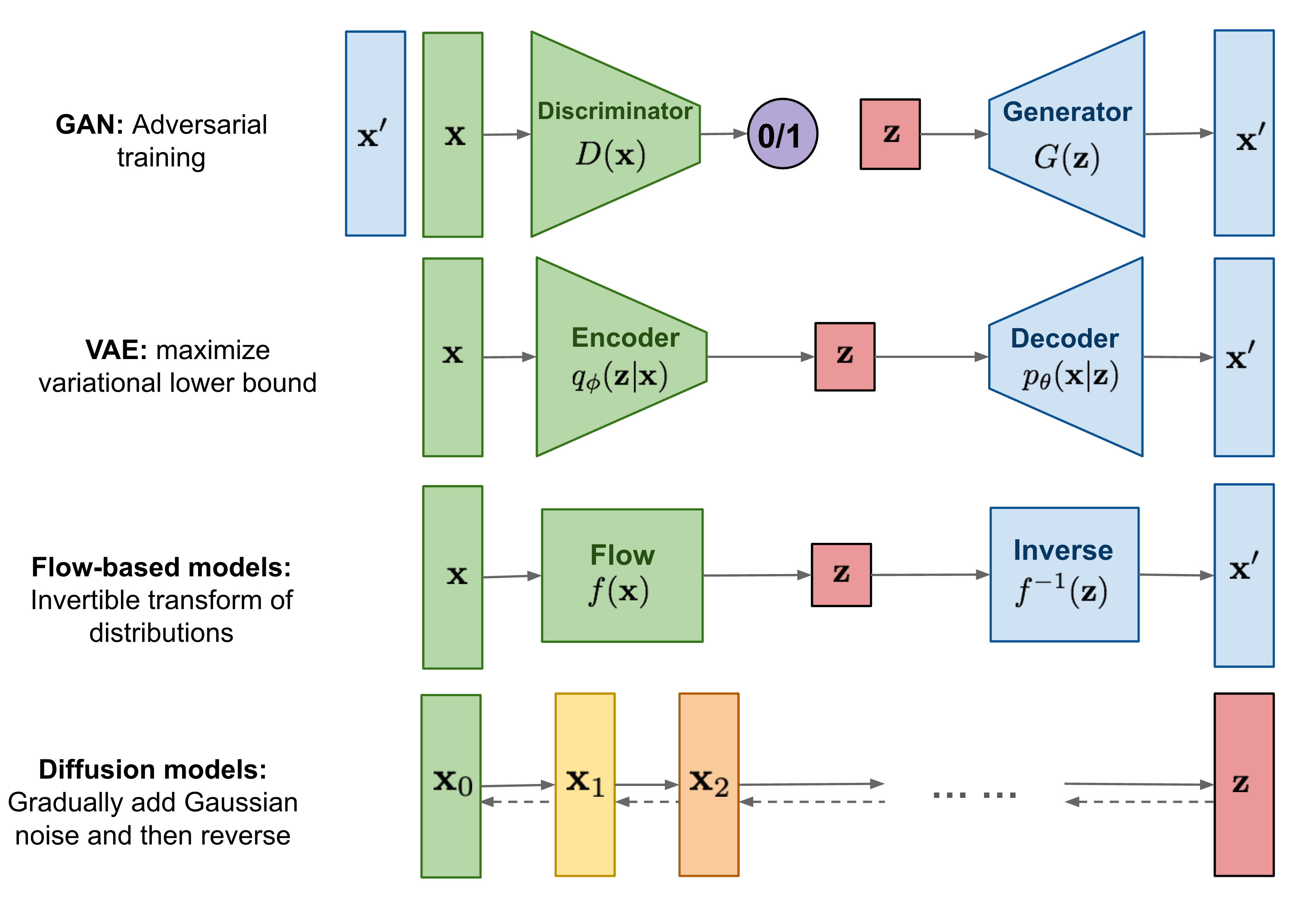
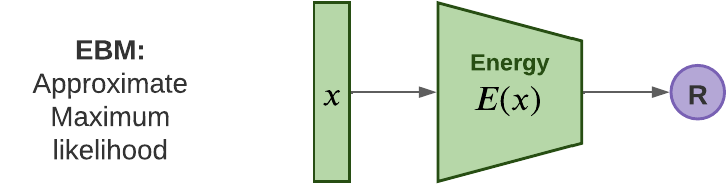
Characteristics of common kinds of generative model, modified from Table 20.1 of Probabilistic Machine Learning: Advanced Topics.

Model	Density	Sampling	Training	Latents	Architecture
VAE	LB, fast	Fast	MLE-LB	${\mathbb{R}}^L$	Encoder-Decoder
ARM	Exact, fast	Slow	MLE	None	Sequential
Flows	Exact, slow/fast	Slow	MLE	${\mathbb{R}}^D$	Invertible
EBM	Approx, slow	Slow	MLE-Approx	Optional	Discriminative
DM	LB	Slow	MLE-LB	${\mathbb{R}}^D$	Encoder-Decoder
GAN	N/A	Fast	Min-max	${\mathbb{R}}^L$	Generator-Discriminator

Community Resources

•  Probabilistic Machine Learning: Advanced Topics (i.e., probml-book2)
  • Chapter 20: Generative models: an overview

---

1. See Section 20.4.1.3 "Likelihood can be hard to compute" from Probabilistic Machine Learning: Advanced Topics ↩

Comments