Diffusion Q-Learning (Diffusion-QL)

Goal: Explore the use of diffusion models to model multi-modal policy distributions in the offline RL domain.

Contribution: Advance the performance on the D4RL benchmark.

Motivation

To prevent generating out-of-distribution actions in offline RL, the literature generally address it by one of the following:

1. regularizing how far the policy can deviate from the behavior policy
2. constraining the learned value function to assign low values to out-of-distribution actions
3. introducing model-based methods, which learn a model of the environment dynamics and perform pessimistic planning in the learned Markov decision process (MDP)
4. treating offline RL as a problem of sequence prediction with return guidance

This work falls in the first category, where its target consist of a behavior-cloning term and a policy improvement term (based on Q-value).

Typically, methods in the first category performs slightly worse than those in the other categories. The underperformance is due to two main reasons:

1. policy classes are not expressive enough
   many methods utilize diagonal Gaussian policies to model multi-modal policies.
2. regularization methods are improper
   Many methods minimize KL-divergence, which may result in mode-covering behavior.

KL-divergence targets require access to explicit density values and MMD targets needs multiple action samples at each state for optimization. Therefore, these targets require an extra step to model the behavior policy of the data, which may further introduce approximation errors.

Concept

The actions are denoted as \(\va_t^i\) or \(\va_t=\va_t^0\), where \(t\) is the timestep in the RL context, and \(i\) is the timestep in the diffusion context.

• Q-value function loss:

  \(\E_{(\vs_t, \va_t, \vs_{t+1}) \sim \gD, \va_{t+1}^0 \sim \pi_{\theta'}} [ \Big|\Big| \big(r(\vs_t, \va_t) + \gamma \min_{i=1,2} Q_{\phi_i'}(\vs_{t+1}, \va_{t+1}^0)\big) - Q_{\phi_i}(\vs_t, \va_t) \Big|\Big|^2 ]\)

• Policy is defined as \(\pi = \argmin\limits_{\pi_\theta} \gL(\theta)\), with loss:
  \(\gL(\theta) = \gL_d(\theta) + \gL_q(\theta) = \gL_d(\theta) - \alpha \cdot \E_{\vs \sim \gD, \va^0 \sim \pi_\theta} [Q_{\phi}(\vs, \va^0)]\), where \(L_d(\theta)\) is the DDPM loss, \(\alpha\) is a balancing factor that scales according to the magnitudes of Q-values in the dataset.

  Please note that the gradient of the Q-value function with respect to the action is backpropagated through the whole diffusion chain.

Diffusion-QL does not explicitly clone the behavioral policy, but implicitly regularized the distance between it with \(L_d(\theta)\).

The full algorithm is shown as follows:

from Algorithm 1 of Wang et al., 2022.

where:

• Equation (1) is the reverse diffusion process of DDPM
• Equation (3) is \(L(\theta)\)
• Equation (4) is the Q-value function loss

Difference with Diffuser

Let a trajectory \(\vtau\) be informally defined as \(\vtau = [\vs_0,\va_0,\dots,\vs_t,\va_t]\).

Diffuser fit a diffusion model to the entire trajectory (i.e., state-action pairs) \(p_\theta(\vtau)\), and learn a separate return model \(J(\vtau)\) to predict the total rewards of each trajectory.

The model generates a full trajectory for each timestep when used online, which is computationally inefficient. i.e., for each step perform:

1. (re-)sample an entire trajectory based on all previous states and actions
2. applies the first action (and record it)
3. discard the generated trajectory in step (1)

Diffusion-QL models \(p_\theta(\va_t|\vs_{0:t-1})\) instead, which applies a conditional diffusion model to the action space, conditioned on the state history. This allow more efficient online planning.

Experiments

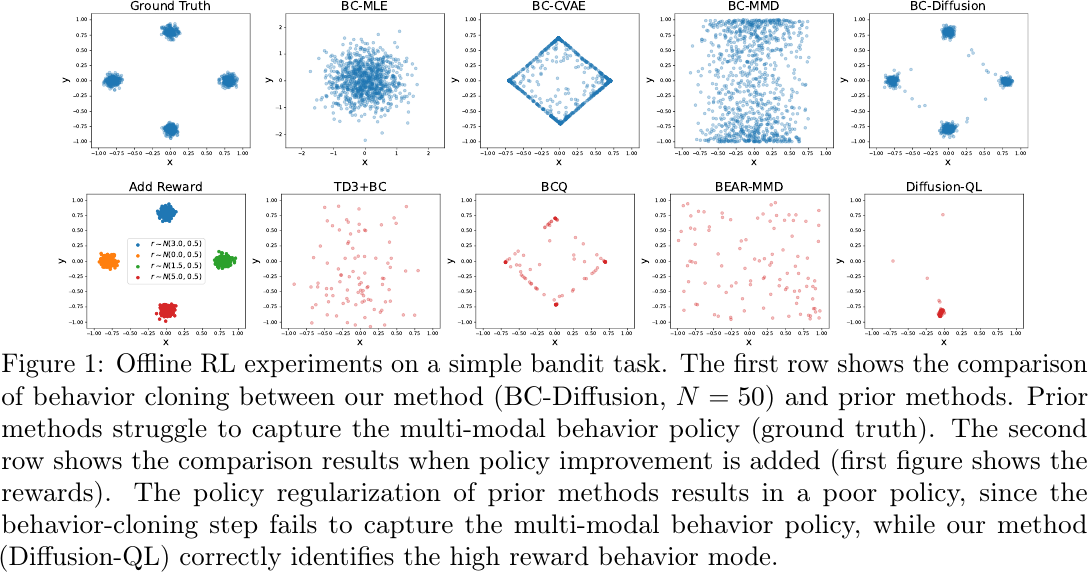
Simple Bandit Task

The bandit task has strong multi-modality.

Offline RL experiments on a simple bandit task, from Figure 1 of Wang et al., 2022.

Experiment examing the effect of varying number of diffusion steps \(N\) on the simple bandit talks, from Figure 2 of Wang et al., 2022.

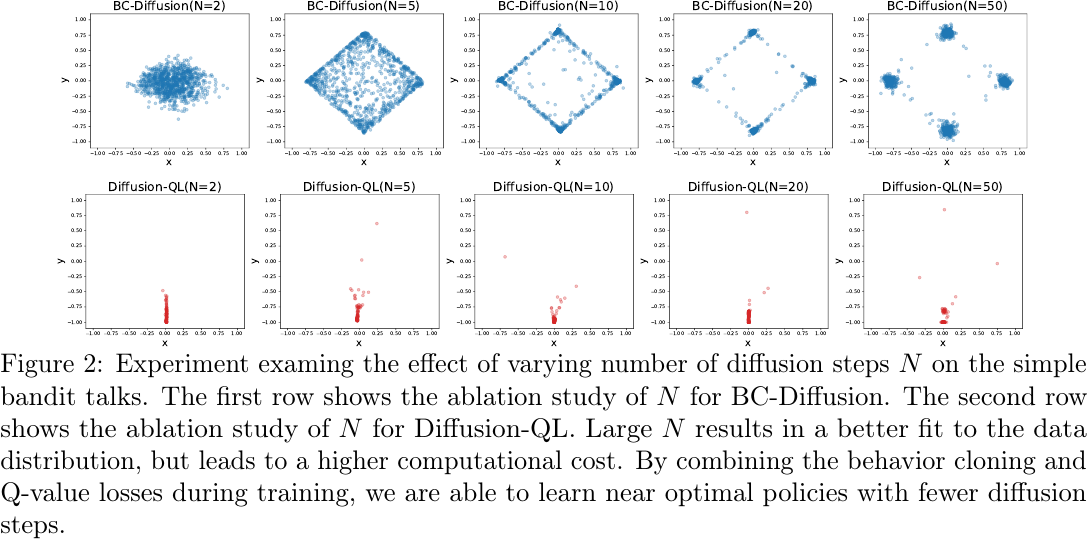
The authors use \(N=5\) in the D4RL dataset.

Benchmark on D4RL

Outperform the baselines on most of the D4RL tasks.

Official Resources

• [ICLR 2023] Diffusion Policies as an Expressive Policy Class for Offline Reinforcement Learning [arxiv][paper][code] (citations:  16,  23, as of 2023-04-28)

Comments