AlphaTensor

Goal: Discover faster (matrix multiplication) algorithms with RL.

Contribution: Discover SOTA algorithms for solving several math problems.

Concept

Overview of AlphaTensor, from DeepMind Blog.

Single-player game played by AlphaTensor, where the goal is to find a correct matrix multiplication algorithm. The state of the game is a cubic array of numbers (shown as grey for 0, blue for 1, and green for -1), representing the remaining work to be done.

1. Formulate the matrix multiplication problem as a tensor decomposition problem.
   This is discussed in previous works such as (Lim 2021, p.67, Example 3.9).

   • Represent a matrix multiplication algorithm as a tensor.

     A \(n\times n\) matrix multiplication algorithm (independent of the matrices being multiplied) can be represented by a fixed 3D (\(n^2\times n^2\times n^2\)) tensor \(\tT_n\) (with entries in \(\{0,1\}\)) called the matrix multiplication tensor (or Strassen's tensor).

     \(\tT_n\) can be constructed trivially based on a simple \(O(n^3)\) matrix multiplication algorithm, with \(m_{(i-1)n+j}=a_ib_j\) and \(c_{(i-1)n+j}\) be the sum of \(n\) terms corresponding to the \(O(n^3)\) algorithm.

   • Execute the matrix multiplication algorithm base on the decomposition of the tensor.

     \(\tT_n=\sum^R_{r=1}\vu^{(r)}\otimes\vv^{(r)}\otimes\vw^{(r)}\), where \(\vu^{(r)},\vv^{(r)},\vw^{(r)}\in\R^{n^2}\) are vectors, and \(\otimes\) denotes the outer (tensor) product. The outer product of each triplet \((\vu^{(r)},\vv^{(r)},\vw^{(r)})\) is a rank-one tensor, and the sum of these \(R\) rank-one tensors results in \(\tT_n\) with \(\mathrm{Rank}(\tT_n)\le R\). Solving the tensor decomposition problem results in an \(O(n^{\log_n(R)})\) algorithm for multiplying arbitrary \(n\times n\) matrices with \(R\) scalar multiplications:

     from Algorithm 1 of Fawzi et al., 2022.

     

     Example: The tensor and its decomposition of Strassen's algorithm (\(R=7\)):

     Matrix multiplication tensor and algorithms, from Fig.1 of Fawzi et al., 2022.

     

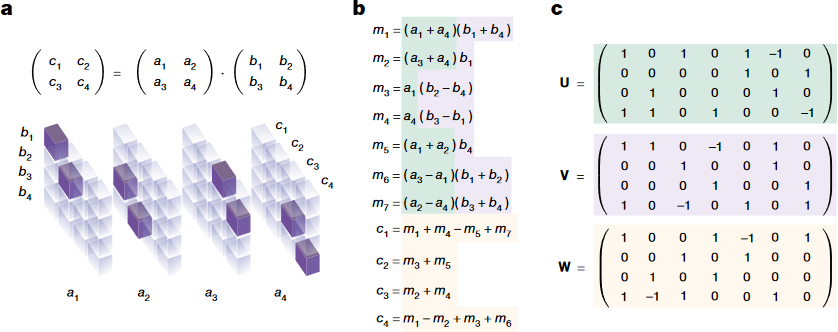
     Please note that the (column) vectors \(\vu^{(r)},\vv^{(r)},\vw^{(r)}\) are stacked horizontally.

     • The elements \(u_{ij}\) in \(\mU\) are indicators for the presence of \(a_i\) in \(m_j\).
     • The elements \(v_{ij}\) in \(\mV\) are indicators for the presence of \(b_i\) in \(m_j\).
     • The elements \(w_{ij}\) in \(\mW\) are indicators for the presence of \(m_j\) in \(c_i\).

2. Formulate the tensor decomposition problem as a game named TensorGame.

   • State: \(S_0=\tT_n, S_t=S_{t-1} - \vu^{(t)}\otimes\vv^{(t)}\otimes\vw^{(t)}\)
   • Action: \(A_t=(\vu^{(t)},\vv^{(t)},\vw^{(t)})\) in canonical form, with coefficients in \(\sF\) (for example \(\sF=\{-2,-1,0,1,2\}\))
   • Terminate Condition: when \(S_t=\bm{0}\) or \(t=T\).
   • Reward: \(R_t=-1\) if \(t\ne T\), \(R_T=-r(S_T)\), where \(r(S_T)\) is an upper bound on the rank of the terminal tensor. The reward function may be modified to optimize practical runtime instead of rank.

3. Solve the TensorGame with DRL and MCTS.

   • Network Architecture:
     • Torso: Modified transformer architecture.
     • Policy head: Transformer architecture.
     • Value head: 4-layer MLP that outputs estimation of certain quantiles.
   • Demonstration Data: Random sample factors \(\{(\vu^{(t)},\vv^{(t)},\vw^{(t)})\}^R_{r=1}\), sum the outer products to construct tensor \(\tD\), and imitate these synthetic demonstrations.
   • Objective: Quantile regression for value network \(z\), and minimize KL-divergence for policy network \(\pi\) (against synthetic demonstration or sample-based improved policy from MCTS).

   • Input Augmentation: Apply random change of basis on \(\tT_n\) before the game (i.e., define the matrix multiplication tensor with another basis). Apply random (signed permutation) change of basis in each new MCTS node.

     Overview of AlphaTensor, from Fig.2 of Fawzi et al., 2022.

     

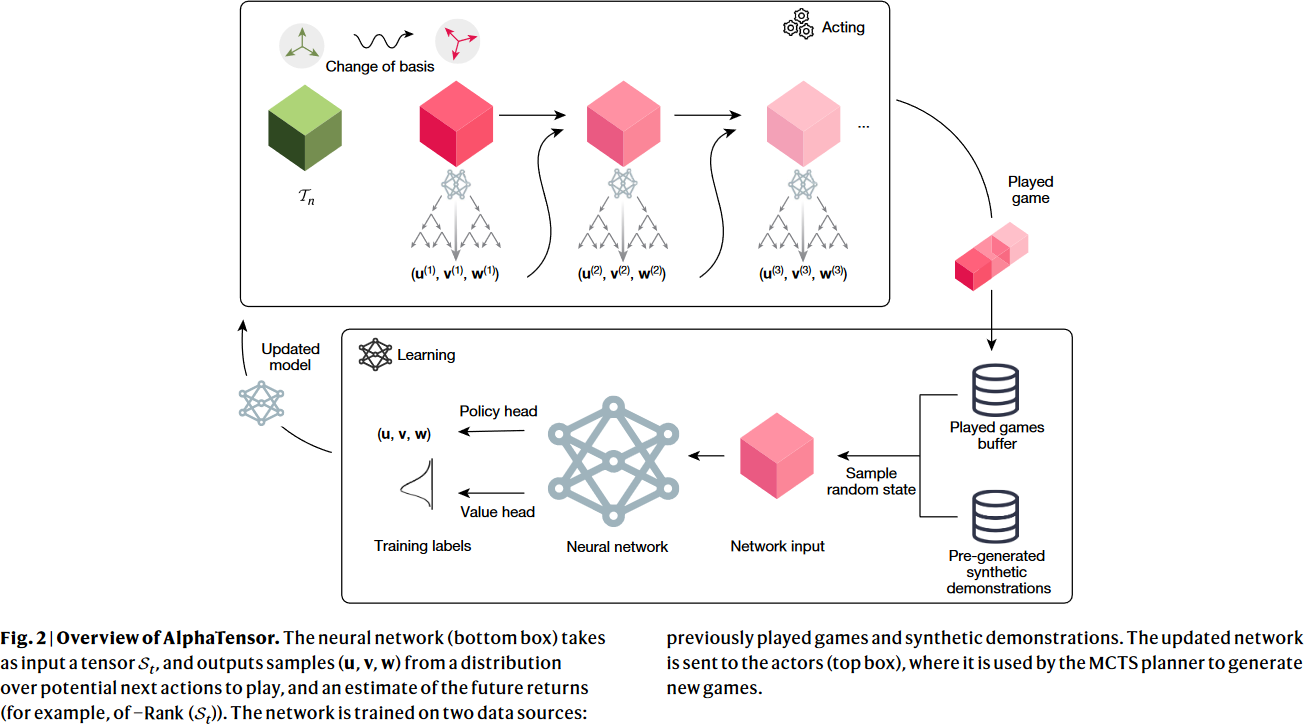
   Please refer to the paper for figures of the architecture.

Results and Costs

• Results
  • SOTA matrix multiplication algorithm for certain size of matrices.
  • SOTA algorithm for multiplying \(n\times n\) skew-symmetric matrices.
  • Re-discover the Fourier basis.
• Training Costs
  • A TPU v3 and TPU v4, takes a week to converge.

Official Resources

• [Nature 2022] Discovering faster matrix multiplication algorithms with reinforcement learning [paper][blog][code] (citations:  98,  78, as of 2023-04-28)

Community Resources

•  [R] Discovering Faster Matrix Multiplication Algorithms With Reinforcement Learning

Comments